
I haven't seen many of these since I left the North Star State.
I'm walking across America.
That's the idea, at least. I'm walking westward from New York City for nine months or so. If everything goes according to plan, I'll be in Oregon when the clock runs out. If nothing goes according to plan, maybe I'll end up in Peru or Mongolia or Pennsylvania. You can read all about the details of my trip if you're so inclined.
Email me at matt@imjustwalkin.com
Subscribe to my email list
Here's my progress so far:
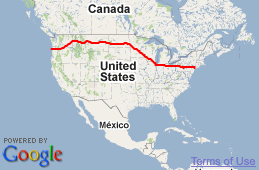

ARE THERE ANY PEDESTRIANS AROUND LOOKS KIND OF LONESOME, BUT A NICE VIEW COMING UP. HANG IN THERE, LOOKS LIKE 2 TO GO BEFORE YOU GET YOU FEET WET WITH SALT WATER.
We do love our trails…
and pop, of course.
Yup – amazing that despite our looong winters, Minneapolis/St. Paul is the #1 city in the USA for bicyclists…we NEED our trails!
baking potatoes as we speak. Minnisota….a brief look back….now walk forward before it is winter….
ps….you could be in washington state by weeks end Matt…..Looks like late august – early September people are in the running for the Pool…..any late entries…may hit me at mattwalkingpool@yahoo.com will post updates when the walking man hits washington. One foot in front of the other ….it is almost a check on the bucket list of life.
Jeff, looks like Matt crossed into Washington state over the weekend, (zoom into the little map)
NAA….Montana, idaho, washington, oregon….Just left Montana and walked into Idaho last night or yesterday late.
He cant be in washington yet. Double check brother. Swear on my kids.
Jeff’s right. I live in the “panhandle” of N. Idaho, and believe me, it DOES exist. ;-) Ten miles West, and I’m in Washington — 50 miles East, and I’m in Montana. Matt only has about 60 – 70 miles until he hits the Eastern Washington “Palouse” region, where it’s almost wheat harvest time. Very different terrain than the last 100 miles. At the fast pace he’s keeping, he will be through Idaho in 2 or 3 days!
Sorry, I meant Idaho not Washington. I stand corrected.
Darnit!
bet no mountains near the ped paths in Minnesota :-)
Matt – I bet the vistas here are beautiful to behold! Safe walking too! I think all states should try and incorporate walking paths. I say try – because I know the economy is bad and funds are low!
We’ve already done that in Washington, Idaho & Montana. Google: “Centennial Trail”, “Trail of the Coeur d’Alenes” and “Route of the Hiawatha” :-)
I believe that is a lefse stand right ahead…and no doubt Sweet Martha’s Cookies…and please lutefisk and Swedish sausage and Swedish meatball’s with mashed potatoes/gravy…oh darn…I guess we’re not in Minnesota anymore…uff da…you betcha…
Don’t forget the Lingonberries and rice for dessert! ; )
Happy to see MN sets the standard for excellence. :-D
We do have some great trails here around the state…
I love our trails here in Minnesota! Lot of them here in the SE MN area as well.
Great Falls has a great paved trail system along the missouri river – that takes you to Giant State Park & Roe River (smallest river), Lewis & Clark Interpative Center, and Many vantage points to see the falls from several locations (40 plus miles of trail ways). Unfortunately he oppted to go straight into town rather than detour slightly to enjoy the walk.